|
| | nmrSVDSolver (void) |
| |
| | nmrSVDSolver (CISSTNETLIB_INTEGER m, CISSTNETLIB_INTEGER n, bool storageOrder) |
| |
| void | Allocate (CISSTNETLIB_INTEGER m, CISSTNETLIB_INTEGER n, bool storageOrder) |
| |
const vctDynamicMatrix
< CISSTNETLIB_DOUBLE > & | GetS (void) const |
| |
const vctDynamicMatrix
< CISSTNETLIB_DOUBLE > & | GetU (void) const |
| |
const vctDynamicMatrix
< CISSTNETLIB_DOUBLE > & | GetVt (void) const |
| |
|
This constructor allocates the memory based on the actual input of the Solve() method. It relies on the method Allocate(). The next call to the Solve() method will check that the parameters match the dimension and storage order.
- Parameters
-
|
| template<class _matrixOwnerType > |
| | nmrSVDSolver (const vctDynamicMatrixBase< _matrixOwnerType, CISSTNETLIB_DOUBLE > &A) |
| |
| template<vct::size_type _rows, vct::size_type _cols, bool _storageOrder> |
| | nmrSVDSolver (const vctFixedSizeMatrix< CISSTNETLIB_DOUBLE, _rows, _cols, _storageOrder > &A) |
| |
|
This methods provide a convenient way to extract the required sizes from the input containers. The next call to the Solve() method will check that the parameters match the dimension.
|
| template<class _matrixOwnerType > |
| void | Allocate (const vctDynamicMatrixBase< _matrixOwnerType, CISSTNETLIB_DOUBLE > &A) |
| |
| template<vct::size_type _rows, vct::size_type _cols, bool _storageOrder> |
| void | Allocate (const vctFixedSizeMatrix< CISSTNETLIB_DOUBLE, _rows, _cols, _storageOrder > &A) |
| |
|
| template<class _matrixOwnerType > |
| void | Solve (vctDynamicMatrixBase< _matrixOwnerType, CISSTNETLIB_DOUBLE > &A) throw (std::runtime_error) |
| |
| template<vct::size_type _rows, vct::size_type _cols, bool _storageOrder> |
| void | Solve (vctFixedSizeMatrix< CISSTNETLIB_DOUBLE, _rows, _cols, _storageOrder > &A) |
| |
Algorithm SVD: Singular Value Decomposition
This computes the singular value decomposition (SVD) of a real 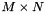 matrix A, optionally computing the left and/or right singular vectors. The SVD is written:
matrix A, optionally computing the left and/or right singular vectors. The SVD is written:
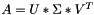
where 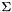 is a
is a 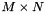 matrix which is zero except for its min(m,n) diagonal elements, U is a
matrix which is zero except for its min(m,n) diagonal elements, U is a 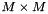 orthogonal matrix, and V is a
orthogonal matrix, and V is a 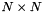 orthogonal matrix. The diagonal elements of
orthogonal matrix. The diagonal elements of 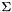 are the singular values of A; they are real and non-negative, and are returned in descending order. The first
are the singular values of A; they are real and non-negative, and are returned in descending order. The first 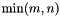 columns of U and V are the left and right singular vectors of A.
columns of U and V are the left and right singular vectors of A.
Note that the routine returns 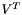 , not
, not 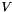 .
.
The data members of this class are:
- M: The number of rows of the input matrix A. M >= 0.
- N: The number of columns of the input matrix A. N >= 0.
- Lda: The leading dimension of the array A.
 .
.
- Ldu: The leading dimension of the array U.
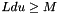 .
.
- Ldvt: The leading dimension of the array VT.
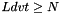 .
.
- Lwork: The dimension of the matrix Work.
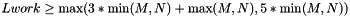 .
.
- Work: Working matrix of dimenstion
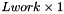 .
.
- S: The singular values of A, sorted so that
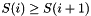 .
.
- U: Contains the
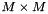 orthogonal matrix U.
orthogonal matrix U.
- Vt: Contains the
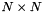 orthogonal matrix
orthogonal matrix 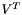 .
.
- A: On entry, the
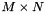 matrix A. On exit, the content of A is altered.
matrix A. On exit, the content of A is altered.
- Note
- The input matrices of this class can use either column major or row major storage order. To select the storage order, use either VCT_COL_MAJOR or VCT_ROW_MAJOR (default) whenever you declare a matrix.
-
The input matrix must be compact (see vctDynamicMatrix::IsCompact() or vctFixedSizeMatrix::IsCompact()).
-
This code relies on the ERC CISST cnetlib library. Since cnetlib is optional, make sure that CISST_HAS_CNETLIB has been turned ON during the configuration with CMake.
- Deprecated:
- This class has been replaced by nmrSVD, nmrSVDDynamicData and nmrSVDFixedSizeData.
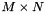 matrix A, optionally computing the left and/or right singular vectors. The SVD is written:
matrix A, optionally computing the left and/or right singular vectors. The SVD is written: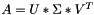
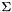 is a
is a 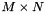 matrix which is zero except for its min(m,n) diagonal elements, U is a
matrix which is zero except for its min(m,n) diagonal elements, U is a 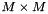 orthogonal matrix, and V is a
orthogonal matrix, and V is a 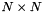 orthogonal matrix. The diagonal elements of
orthogonal matrix. The diagonal elements of 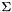 are the singular values of A; they are real and non-negative, and are returned in descending order. The first
are the singular values of A; they are real and non-negative, and are returned in descending order. The first 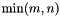 columns of U and V are the left and right singular vectors of A.
columns of U and V are the left and right singular vectors of A.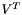 , not
, not 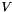 .
. .
.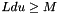 .
.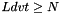 .
.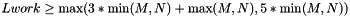 .
.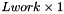 .
.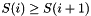 .
.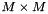 orthogonal matrix U.
orthogonal matrix U.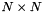 orthogonal matrix
orthogonal matrix 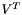 .
.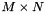 matrix A. On exit, the content of A is altered.
matrix A. On exit, the content of A is altered.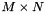 matrix A, optionally computing the left and/or right singular vectors. The SVD is written:
matrix A, optionally computing the left and/or right singular vectors. The SVD is written: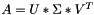
 1.8.6
1.8.6