Declaration of vctEulerRotation3. More...

#include <cisstCommon/cmnConstants.h>
#include <cisstVector/vctForwardDeclarations.h>
#include <cisstVector/vctFixedSizeVectorTypes.h>
#include <cisstVector/vctExport.h>

Classes
class	vctEulerRotation3Base

class	vctEulerRotation3< _order >

Namespaces
	vctEulerRotation3Order

Macros
#define	VCT_DECLARE_EULER_CONVERSIONS(ORDER)
	Define an Euler angle rotation for a space of dimension 3. More...

Typedefs
typedef vctEulerRotation3 < vctEulerRotation3Order::ZYZ >	vctEulerZYZRotation3

typedef vctEulerRotation3 < vctEulerRotation3Order::ZYX >	vctEulerZYXRotation3

Functions
std::string CISST_EXPORT	vctEulerRotation3Order::ToString (vctEulerRotation3Order::OrderType order)

Detailed Description

Declaration of vctEulerRotation3.

Macro Definition Documentation

#define VCT_DECLARE_EULER_CONVERSIONS ( ORDER )

Value:

template <class _matrixType> \
    void \
    vctEulerFromMatrixRotation3(vctEulerRotation3<ORDER> & eulerRot, \
                        const vctMatrixRotation3Base<_matrixType> & matrixRot); \
    template <class _matrixType> \
    void \
    vctEulerToMatrixRotation3(const vctEulerRotation3<ORDER> & eulerRot, \
                      vctMatrixRotation3Base<_matrixType> & matrixRot);

Define an Euler angle rotation for a space of dimension 3.

There are several conventions for Euler angle rotations, which depend on the order of rotations about the axes, and whether the rotations are intrinsic (i.e., about the body's coordinate frame) or extrinsic (i.e., about the world coordinate frame).

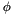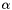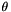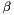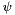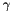We use the common convention of three letters to define the order of (intrinsic) rotations. For example, ZYZ refers to a rotation of $\phi$ (or $\alpha$ ) about Z, followed by a rotation of $\theta$ (or $\beta$ ) about Y', followed by a rotation of $\psi$ (or $\gamma$ ) about Z''. Here, the Y' and Z'' denote that the rotations are about the new (rotated) Y and Z axes, respectively. For convenience (and to conform to C++ naming rules), the ' and '' are omitted from the naming convention. Note that when composing intrinsic rotations, the order is as follows: 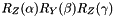$R_Z(\alpha) R_Y(\beta) R_Z(\gamma)$ . All angles are in radians.

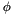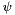The range of angles must still be determined. One possibility is to have $\phi$ and $\psi$ be in the range ( 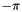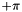$-\pi$ , $+\pi$ ], and 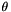$\theta$ is in the range [0, 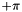$+\pi$ ]. For now, the IsNormalized method always returns true.

Because there are so many possible Euler angle conventions, we implement a base class, vctEulerRotation3, and then specialize it with derived classes that are templated by the vctEulerRotation3Order::OrderType enum (see vctForwardDeclarations.h).

Note that we could have also templated the Euler angle class by element type (double or float), but decided that this was not worthwhile – all Euler angle rotation classes use double.

Typedef Documentation

typedef vctEulerRotation3<vctEulerRotation3Order::ZYX> vctEulerZYXRotation3

Define an Euler angle rotation in dimension 3 using ZYX (yaw-pitch-roll) order.

typedef vctEulerRotation3<vctEulerRotation3Order::ZYZ> vctEulerZYZRotation3

Define an Euler angle rotation in dimension 3 using ZYZ order.

Classes

Namespaces

Macros

Typedefs

Functions

Detailed Description

Macro Definition Documentation

Typedef Documentation