|
cisst-saw
|
|
cisst-saw
|
#include <nmrLSISolver.h>
Public Member Functions | |
| nmrLSISolver (void) | |
| nmrLSISolver (CISSTNETLIB_INTEGER ma, CISSTNETLIB_INTEGER na, CISSTNETLIB_INTEGER mg) | |
| nmrLSISolver (vctDynamicMatrix< CISSTNETLIB_DOUBLE > &C, vctDynamicMatrix< CISSTNETLIB_DOUBLE > &d, vctDynamicMatrix< CISSTNETLIB_DOUBLE > &A, vctDynamicMatrix< CISSTNETLIB_DOUBLE > &b) | |
| void | Allocate (CISSTNETLIB_INTEGER ma, CISSTNETLIB_INTEGER na, CISSTNETLIB_INTEGER mg) |
| void | Allocate (vctDynamicMatrix< CISSTNETLIB_DOUBLE > &C, vctDynamicMatrix< CISSTNETLIB_DOUBLE > &d, vctDynamicMatrix< CISSTNETLIB_DOUBLE > &A, vctDynamicMatrix< CISSTNETLIB_DOUBLE > &b) |
| CISST_EXPORT void | Solve (vctDynamicMatrix< CISSTNETLIB_DOUBLE > &C, vctDynamicMatrix< CISSTNETLIB_DOUBLE > &d, vctDynamicMatrix< CISSTNETLIB_DOUBLE > &A, vctDynamicMatrix< CISSTNETLIB_DOUBLE > &b) throw (std::runtime_error) |
| const vctDynamicMatrix < CISSTNETLIB_DOUBLE > & | GetX (void) const |
Protected Attributes | |
| CISSTNETLIB_INTEGER | Ma |
| CISSTNETLIB_INTEGER | Na |
| CISSTNETLIB_INTEGER | Mg |
| vctDynamicMatrix < CISSTNETLIB_DOUBLE > | VSiUtb |
| vctDynamicMatrix < CISSTNETLIB_DOUBLE > | GTilde |
| vctDynamicMatrix < CISSTNETLIB_DOUBLE > | HTilde |
| vctDynamicMatrix < CISSTNETLIB_DOUBLE > | Z |
| vctDynamicMatrix < CISSTNETLIB_DOUBLE > | X |
| vctDynamicMatrix < CISSTNETLIB_DOUBLE > | Si |
| vctDynamicMatrix < CISSTNETLIB_DOUBLE > | VSi |
| nmrSVDRSSolver | SVDRS |
| nmrLDPSolver | LDP |
Algorithm LSI: Least Squares with Inequality Constraints.
This code is a re-written version of algorithm from Charles L. Lawson and Richard J. Hanson, "Solving Least Squares Problems", Prentice-Hall, 1974. Section 5: Chapter 23.
Given a 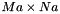 matrix C, a
matrix C, a 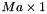 vector d, a
vector d, a 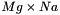 A and a
A and a 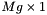 vector b, compute a
vector b, compute a 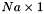 vector X, that solves the least squares problem:
vector X, that solves the least squares problem:
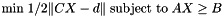
The data members of this class are:
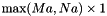 contains
contains 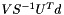
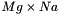 contains
contains 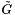 . See L&H book for definition of
. See L&H book for definition of 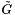 .
.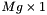 contains
contains 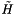 . See L&H book for definition of
. See L&H book for definition of 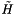 .
.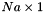 contains solution of the internal LDP problem
contains solution of the internal LDP problem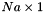 , on exit contains the solution.
, on exit contains the solution.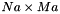 contains the pseudo inverse of singular values.
contains the pseudo inverse of singular values.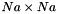 contains
contains 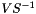
|
inline |
Default constructor. This constructor doesn't allocate any memory. If you use this constructor, you will need to use one of the Allocate() methods before you can use the Solve method.
|
inline |
Constructor with memory allocation. This constructor allocates the memory based on Ma, Na and Mg. It relies on the method Allocate(). The next call to the Solve() method will check that the parameters match the dimension.
| ma | Number of rows of C |
| na | Number of columns of C |
| mg | Number of rows of A |
|
inline |
Constructor with memory allocation. This constructor allocates the memory based on the actual input of the Solve() method. It relies on the method Allocate(). The next call to the Solve() method will check that the parameters match the dimension.
|
inline |
This method allocates the memory based on Ma, Na and Mg. The next call to the Solve() method will check that the parameters match the dimension.
| ma | Number of rows of C |
| na | Number of columns of C |
| mg | Number of rows of A |
|
inline |
Allocate memory to solve this problem. This method provides a convenient way to extract the required sizes from the input containers. The next call to the Solve() method will check that the parameters match the dimension.
|
inline |
Get X. This method must be used after Solve().
| CISST_EXPORT void nmrLSISolver::Solve | ( | vctDynamicMatrix< CISSTNETLIB_DOUBLE > & | C, |
| vctDynamicMatrix< CISSTNETLIB_DOUBLE > & | d, | ||
| vctDynamicMatrix< CISSTNETLIB_DOUBLE > & | A, | ||
| vctDynamicMatrix< CISSTNETLIB_DOUBLE > & | b | ||
| ) | |||
| throw | ( | std::runtime_error | |
| ) | |||
Given a 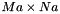 matrix C, a
matrix C, a 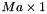 vector d, a
vector d, a 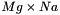 A and a
A and a 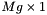 vector b, compute a
vector b, compute a 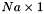 vector X, that solves the least squares problem:
vector X, that solves the least squares problem:
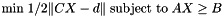
|
protected |
|
protected |
|
protected |
|
protected |
|
protected |
|
protected |
|
protected |
|
protected |
|
protected |
|
protected |
|
protected |
|
protected |
 1.8.6
1.8.6