Algorithm SVDRS: Singular Value Decomposition also treating Right Side Vector.
The original version of this code was developed by Charles L. Lawson and Richard J. Hanson at Jet Propulsion Laboratory 1974 SEP 25, and published in the book "Solving Least Squares Problems", Prentice-Hall, 1974.
This subroutine computes the singular value decomposition of the given 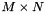 matrix A, and optionally applies the transformations from the left to the
matrix A, and optionally applies the transformations from the left to the 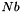 column vectors of the
column vectors of the 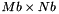 matrix B. Either
matrix B. Either 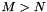 or
or 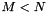 is permitted.
is permitted.
The singular value decomposition of A is of the form:
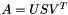
where U is 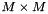 orthogonal, S is
orthogonal, S is 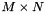 diagonal with the diagonal terms nonnegative and ordered from large to small, and V is
diagonal with the diagonal terms nonnegative and ordered from large to small, and V is 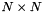 orthogonal. Note that these matrices also satisfy:
orthogonal. Note that these matrices also satisfy:
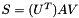
The singular values, i.e. the diagonal terms of the matrix S, are returned in the matrix GetS(). If 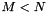 , positions
, positions 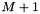 through N of S() will be set to zero.
through N of S() will be set to zero.
The product matrix 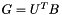 replaces the given matrix B in the matrix B(,).
replaces the given matrix B in the matrix B(,).
If the user wishes to obtain a minimum length least squares solution of the linear system:
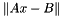
the solution X can be constructed, following use of this subroutine, by computing the sum for i = 1, ..., R of the outer products
(Col i of V) * (1/S(i)) * (Row i of G)
Here R denotes the pseudorank of A which the user may choose in the range 0 through 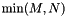 based on the sizes of the singular values.
based on the sizes of the singular values.
The data members of this class are:
- M: Number of rows of matrix A, B, G.
- N: Number of columns of matrix A. No of rows and columns of matrix V.
- Lda: First dimensioning parameter for A.
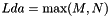
- Ldb: First dimensioning parameter for B.
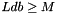
- Nb: Number of columns in the matrices B and G.
- A: On input contains the
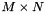 matrix A. On output contains the
matrix A. On output contains the 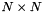 matrix V.
matrix V.
- B: If
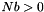 this array must contain a
this array must contain a 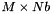 matrix on input and will contain the
matrix on input and will contain the 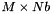 product matrix,
product matrix, 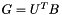 on output.
on output.
- S: On return will contain the singular values of A, with the ordering
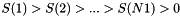 . If
. If 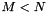 the singular values indexed from
the singular values indexed from 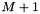 through N will be zero.
through N will be zero.
- Work Work space of total size at least
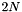 .
.
- Note
- This code gives special treatment to rows and columns that are entirely zero. This causes certain zero singular values to appear as exact zeros rather than as about MACHEPS times the largest singular value It similarly cleans up the associated columns of U and V.
-
The input matrices of this class must use a column major storage order. To do so, use VCT_COL_MAJOR whenever you declare a matrix. They must also be compact (see vctDynamicMatrix::IsFortran()).
-
This code relies on the ERC CISST cnetlib library. Since cnetlib is optional, make sure that CISST_HAS_CNETLIB has been turned ON during the configuration with CMake.
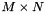 matrix A, and optionally applies the transformations from the left to the
matrix A, and optionally applies the transformations from the left to the 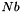 column vectors of the
column vectors of the 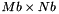 matrix B. Either
matrix B. Either 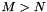 or
or 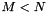 is permitted.
is permitted.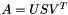
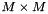 orthogonal, S is
orthogonal, S is 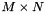 diagonal with the diagonal terms nonnegative and ordered from large to small, and V is
diagonal with the diagonal terms nonnegative and ordered from large to small, and V is 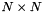 orthogonal. Note that these matrices also satisfy:
orthogonal. Note that these matrices also satisfy: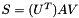
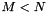 , positions
, positions 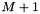 through N of S() will be set to zero.
through N of S() will be set to zero.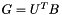 replaces the given matrix B in the matrix B(,).
replaces the given matrix B in the matrix B(,).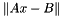
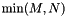 based on the sizes of the singular values.
based on the sizes of the singular values.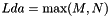
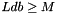
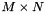 matrix A. On output contains the
matrix A. On output contains the 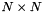 matrix V.
matrix V.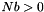 this array must contain a
this array must contain a 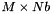 matrix on input and will contain the
matrix on input and will contain the 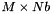 product matrix,
product matrix, 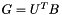 on output.
on output.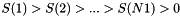 . If
. If 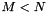 the singular values indexed from
the singular values indexed from 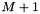 through N will be zero.
through N will be zero.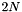 .
.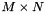 matrix A, and optionally applies the transformations from the left to the
matrix A, and optionally applies the transformations from the left to the 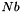 column vectors of the
column vectors of the 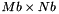 matrix B. Either
matrix B. Either 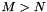 or
or 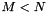 is permitted.
is permitted.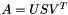
 1.8.6
1.8.6