#include <nmrLSNonLinSolver.h>

Public Member Functions
	nmrLSNonLinSolver (void)

	nmrLSNonLinSolver (CISSTNETLIB_INTEGER m, CISSTNETLIB_INTEGER n)

void	Allocate (CISSTNETLIB_INTEGER m, CISSTNETLIB_INTEGER n)


	nmrLSNonLinSolver (vctDynamicVector< CISSTNETLIB_DOUBLE > &X, vctDynamicVector< CISSTNETLIB_DOUBLE > &F)


void	Allocate (vctDynamicVector< CISSTNETLIB_DOUBLE > &X, vctDynamicVector< CISSTNETLIB_DOUBLE > &F)


template<int __instanceLine, class __elementType >
void	Solve (nmrCallBackFunctionF< __instanceLine, __elementType > &callBack, vctDynamicVector< CISSTNETLIB_DOUBLE > &X, vctDynamicVector< CISSTNETLIB_DOUBLE > &F, CISSTNETLIB_DOUBLE tolerance) throw (std::runtime_error)

Protected Attributes
CISSTNETLIB_INTEGER	M

CISSTNETLIB_INTEGER	N

CISSTNETLIB_DOUBLE	Tolerance

CISSTNETLIB_INTEGER	Info

CISSTNETLIB_INTEGER	Lwork

vctDynamicVector < CISSTNETLIB_INTEGER >	IWork

vctDynamicVector < CISSTNETLIB_DOUBLE >	Work

Detailed Description

Algorithm LSNonLin: Non Linear Least Squares by Levenberg Marquardt method The purpose of this is to minimize the sum of the squares of M nonlinear functions in N variables by a modification of the levenberg-marquardt algorithm. The user must provide a subroutine which calculates the functions. The jacobian is then calculated by a forward-difference approximation.

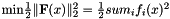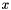Rather than compute the value f(x) (the sum of squares), LSNonLin requires the user-defined function to compute the vector-valued function. $\textbf{F}(x) = [f_1(x), f_2(x), f_3(x)]^{t}$ Then, in vector terms, you can restate this optimization problem as $\mbox{min} \frac{1}{2} \| \textbf{F}(x) \|_2^2 = \frac{1}{2} sum_i f_i(x)^2$ where $x$ is a vector and 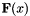$\textbf{F}(x)$ is a function that returns a vector value.

The data members of this class are:

M: The number of nonlinear functions M >= 0.
N: The number of variables. N >= 0.
Tolerance: A nonnegative input variable. Termination occurs when the algorithm estimates either that the relative error in the sum of squares is at most Tolerance or that the relative error between X and the solution is at most Tolerance. (Default set to 1.0e-6).
IWork: An integer working vector of length N.
Work: A working vector of length M*N+5*N+M.
LWork: Length of working array.

Info: = info is an integer output variable. if the user has terminated execution, info is set to the (negative) value of Flag. see description of callBack. otherwise, info is set as follows.

info = 0  improper input parameters.

info = 1  algorithm estimates that the relative error
          in the sum of squares is at most tol.

info = 2  algorithm estimates that the relative error
          between x and the solution is at most tol.

info = 3  conditions for info = 1 and info = 2 both hold.

info = 4  fvec is orthogonal to the columns of the
          jacobian to machine precision.

info = 5  number of calls to fcn has reached or
          exceeded 200*(n+1).

info = 6  tol is too small. no further reduction in
          the sum of squares is possible.

info = 7  tol is too small. no further improvement in
          the approximate solution x is possible

The input/output from this class is:

X: On entry, the inital estimate of solution vector. On exit, final estimate of solution vector.
RNorm: If used, the value of the squared 2-norm of the residual at final value of x
callBack: Is object of type nmrCallBackLSNonLinSolver used to supply the user method. The user method which belongs to a user defined class 'Cfoo' has the following definition int Cfoo::Mbar (vctDynamicVectorRef<CISSTNETLIB_DOUBLE> &X, vctDynamicVectorRef<CISSTNETLIB_DOUBLE> &F, CISSTNETLIB_INTEGER &Flag); The solver calls this method when needed to obtain values for F for a given variable values X. the value of Flag should not be changed by Mbar unless the user wants to terminate execution of Solver. in this case set Flag to a negative integer.

The following constructor can be used to contruct the nmrCallBackLSNonLinSolver object required to be passed to the Solve() method. This object needs to be created only once per given set of nonlinear functions to be minized. nmrCallBackLSNonLinSolver<nmrUNIQUE_IDENTIFIER_LINE, Cfoo> callBackObject(this, &Cfoo::Mbar);

Note: This code relies on the ERC CISST cnetlib library. Since cnetlib is optional, make sure that CISST_HAS_CNETLIB has been turned ON during the configuration with CMake.

Constructor & Destructor Documentation

nmrLSNonLinSolver::nmrLSNonLinSolver ( void )

inline

Default constructor. This constructor doesn't allocate any memory. If you use this constructor, you will need to use one of the Allocate() methods before you can use the Solve method.

nmrLSNonLinSolver::nmrLSNonLinSolver	(	CISSTNETLIB_INTEGER	m,
		CISSTNETLIB_INTEGER	n
	)

inline

Constructor with memory allocation. This constructor allocates the memory based on M and N. It relies on the method Allocate(). The next call to the Solve() method will check that the parameters match the dimension.

Parameters

m	Number of nonlinear functions.
n	Number of variables This order will be used for the output as well.

nmrLSNonLinSolver::nmrLSNonLinSolver	(	vctDynamicVector< CISSTNETLIB_DOUBLE > &	X,
		vctDynamicVector< CISSTNETLIB_DOUBLE > &	F
	)

inline

Constructor with memory allocation. This constructor allocates the memory based on the actual input of the Solve() method. It relies on the method Allocate(). The next call to the Solve() method will check that the parameters match the dimension and storage order.

Member Function Documentation

void nmrLSNonLinSolver::Allocate	(	CISSTNETLIB_INTEGER	m,
		CISSTNETLIB_INTEGER	n
	)

inline

This method allocates the memory based on M and N. The next call to the Solve() method will check that the parameters match the dimension.

Parameters

m	Number of nonlinear functions
n	Number of variables

void nmrLSNonLinSolver::Allocate	(	vctDynamicVector< CISSTNETLIB_DOUBLE > &	X,
		vctDynamicVector< CISSTNETLIB_DOUBLE > &	F
	)

inline

Allocate memory to solve this problem. This method provides a convenient way to extract the required sizes from the input containers. The next call to the Solve() method will check that the parameters match the dimension.

template<int __instanceLine, class __elementType >

void nmrLSNonLinSolver::Solve	(	nmrCallBackFunctionF< __instanceLine, __elementType > &	callBack,
		vctDynamicVector< CISSTNETLIB_DOUBLE > &	X,
		vctDynamicVector< CISSTNETLIB_DOUBLE > &	F,
		CISSTNETLIB_DOUBLE	tolerance
	)
throw	(	std::runtime_error
	)

inline

This computes the solves nonlinear least squares problem invloving M functions in N variables. On input, X contains the starting point, On output, X contains the final estimate, F contrains the final value

Member Data Documentation

CISSTNETLIB_INTEGER nmrLSNonLinSolver::Info

protected

vctDynamicVector<CISSTNETLIB_INTEGER> nmrLSNonLinSolver::IWork

protected

CISSTNETLIB_INTEGER nmrLSNonLinSolver::Lwork

protected

CISSTNETLIB_INTEGER nmrLSNonLinSolver::M

protected

CISSTNETLIB_INTEGER nmrLSNonLinSolver::N

protected

CISSTNETLIB_DOUBLE nmrLSNonLinSolver::Tolerance

protected

vctDynamicVector<CISSTNETLIB_DOUBLE> nmrLSNonLinSolver::Work

protected

The documentation for this class was generated from the following file:

/home/adeguet1/catkin_ws/src/cisst-saw/cisst/cisstNumerical/nmrLSNonLinSolver.h

Public Member Functions

Protected Attributes

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation