|
| | nmrLSNonLinJacobianSolver (void) |
| |
| | nmrLSNonLinJacobianSolver (CISSTNETLIB_INTEGER m, CISSTNETLIB_INTEGER n) |
| |
| void | Allocate (CISSTNETLIB_INTEGER m, CISSTNETLIB_INTEGER n) |
| |
|
| | nmrLSNonLinJacobianSolver (vctDynamicVector< CISSTNETLIB_DOUBLE > &X, vctDynamicVector< CISSTNETLIB_DOUBLE > &F) |
| |
|
| void | Allocate (vctDynamicVector< CISSTNETLIB_DOUBLE > &X, vctDynamicVector< CISSTNETLIB_DOUBLE > &F) |
| |
|
| template<int __instanceLineF, class __elementTypeF , int __instanceLineJ, class __elementTypeJ > |
| void | Solve (nmrCallBackFunctionF< __instanceLineF, __elementTypeF > &callBackF, nmrCallBackFunctionJ< __instanceLineJ, __elementTypeJ > &callBackJ, vctDynamicVector< CISSTNETLIB_DOUBLE > &X, vctDynamicVector< CISSTNETLIB_DOUBLE > &F, vctDynamicVector< CISSTNETLIB_DOUBLE > &J, CISSTNETLIB_DOUBLE tolerance) throw (std::runtime_error) |
| |
Algorithm LSNonLin: Non Linear Least Squares by Levenberg Marquardt method The purpose of this is to minimize the sum of the squares of M nonlinear functions in N variables by a modification of the levenberg-marquardt algorithm. The user must provide a subroutine which calculates the functions. The user must provide a subroutine which calculates the functions and the jacobian
Rather than compute the value f(x) (the sum of squares), LSNonLin requires the user-defined function to compute the vector-valued function. ![$ \textbf{F}(x) = [f_1(x), f_2(x), f_3(x)]^{t} $](../../form_182.png) Then, in vector terms, you can restate this optimization problem as
Then, in vector terms, you can restate this optimization problem as 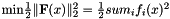 where
where 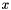 is a vector and
is a vector and 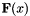 is a function that returns a vector value.
is a function that returns a vector value.
The data members of this class are:
The input/output from this class is:
- X: On entry, the inital estimate of solution vector. On exit, final estimate of solution vector.
- RNorm: If used, the value of the squared 2-norm of the residual at final value of x
- callBack: Is object of type nmrCallBackLSNonLinSolver used to supply the user method. The user method which belongs to a user defined class 'Cfoo' has the following definition int Cfoo::Mbar (vctDynamicVectorRef<CISSTNETLIB_DOUBLE> &X, vctDynamicVectorRef<CISSTNETLIB_DOUBLE> &F, vctDynamicMatrixRef<CISSTNETLIB_DOUBLE> &J, CISSTNETLIB_INTEGER &Flag) if Flag = 1 calculate the functions at X and return this vector in F. do not alter J. if Flag = 2 calculate the jacobian at X and return this matrix in J. do not alter F. the value of Flag should not be changed by Mbar unless the user wants to terminate execution of Solver. in this case set Flag to a negative integer.
The solver calls this method when needed to obtain values for F for
a given variable values X.
The following constructor can be used to contruct the nmrCallBackLSNonLinSolver object
required to be passed to the Solve() method. This object needs to be created
only once per given set of nonlinear functions to be minized.
nmrCallBackLSNonLinSolver<nmrUNIQUE_IDENTIFIER_LINE, Cfoo> callBackObject(this, &Cfoo::Mbar);
- Note
- This code relies on the ERC CISST cnetlib library. Since cnetlib is optional, make sure that CISST_HAS_CNETLIB has been turned ON during the configuration with CMake.
![$ \textbf{F}(x) = [f_1(x), f_2(x), f_3(x)]^{t} $](../../form_182.png) Then, in vector terms, you can restate this optimization problem as
Then, in vector terms, you can restate this optimization problem as 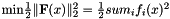 where
where 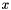 is a vector and
is a vector and 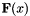 is a function that returns a vector value.
is a function that returns a vector value. 1.8.6
1.8.6