|
| | nmrLSSolver (void) |
| |
| | nmrLSSolver (CISSTNETLIB_INTEGER m, CISSTNETLIB_INTEGER n, CISSTNETLIB_INTEGER nrhs, bool storageOrder) |
| |
| void | Allocate (CISSTNETLIB_INTEGER m, CISSTNETLIB_INTEGER n, CISSTNETLIB_INTEGER nrhs, bool storageOrder) |
| |
|
| | nmrLSSolver (vctDynamicMatrix< double > &A, vctDynamicMatrix< double > &B) |
| |
|
| void | Allocate (vctDynamicMatrix< double > &A, vctDynamicMatrix< double > &B) |
| |
|
| template<class _matrixOwnerType > |
| void | Solve (vctDynamicMatrixBase< _matrixOwnerType, double > &A, vctDynamicMatrixBase< _matrixOwnerType, double > &B) throw (std::runtime_error) |
| |
Algorithm LS: Least Squares by QR or LQ decomposition This solves overdetermined or underdetermined real linear systems involving an M-by-N matrix A, or its transpose, using a QR or LQ factorization of A. It is assumed that A has full rank.
The following options are provided:
- If m >= n: find the least squares solution of an overdetermined system, i.e., solve the least squares problem
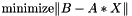
- If m < n: find the minimum norm solution of an underdetermined system
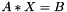
The data members of this class are:
- M: The number of rows of the input matrix A.
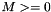 .
.
- N: The number of columns of the input matrix A.
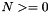 .
.
- NRHS: The number of right hand sides, i.e., the number of columns of the matrices B and X.
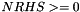 .
.
- Lda: The leading dimension of the array A.
 .
.
- Ldb: The leading dimension of the array B.
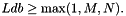 .
.
- Lwork: The dimension of the matrix Work.
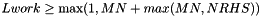 . For optimal performance,
. For optimal performance, 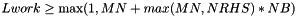 . where
. where 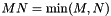 and
and 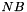 is the optimum block size.
is the optimum block size.
- Info: = 0: successful exit < 0: argument had an illegal value
- Work: Working matrix of dimenstion
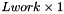 .
.
The input/output from this class is:
- A: On entry, the
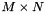 matrix A. On exit, if M >= N, A is overwritten by details of its QR factorization if M < N, A is overwritten by details of its LQ factorization
matrix A. On exit, if M >= N, A is overwritten by details of its QR factorization if M < N, A is overwritten by details of its LQ factorization
- B: On entry, the matrix B of right hand side vectors, stored columnwise; B is M-by-NRHS On exit, B is overwritten by the solution vectors, stored columnwise: if m >= n, rows 1 to n of B contain the least squares solution vectors; the residual sum of squares for the solution in each column is given by the sum of squares of elements N+1 to M in that column; if m < n, rows 1 to N of B contain the minimum norm solution vectors;
- Note
- The input matrix must be compact (see vctDynamicMatrix::IsCompact() or vctFixedSizeMatrix::IsCompact()).
-
This code relies on the ERC CISST cnetlib library. Since cnetlib is optional, make sure that CISST_HAS_CNETLIB has been turned ON during the configuration with CMake.
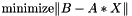
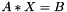
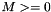 .
.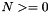 .
.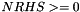 .
. .
.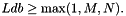 .
.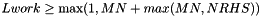 . For optimal performance,
. For optimal performance, 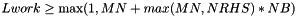 . where
. where 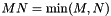 and
and 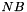 is the optimum block size.
is the optimum block size.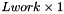 .
.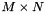 matrix A. On exit, if M >= N, A is overwritten by details of its QR factorization if M < N, A is overwritten by details of its LQ factorization
matrix A. On exit, if M >= N, A is overwritten by details of its QR factorization if M < N, A is overwritten by details of its LQ factorization 1.8.6
1.8.6