cisst-saw
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Groups Pages
Public Types | Public Member Functions | Static Public Member Functions | Protected Attributes | List of all members
nmrPolynomialTermPowerIndex Class Reference
cisstNumerical

Represents the power index of a single term in a multi-variable polynomial. More...

#include <nmrPolynomialTermPowerIndex.h>

Public Types

typedef int VariableIndexType
 
typedef int PowerType
 
typedef unsigned long MultinomialCoefficientType
 

Public Member Functions

 nmrPolynomialTermPowerIndex (VariableIndexType numVariables=1, PowerType minDegree=0, PowerType maxDegree=4)
 
 nmrPolynomialTermPowerIndex (const nmrPolynomialBase &p)
 
int GetDegree () const
 
PowerType GetMaxDegree () const
 
PowerType GetMinDegree () const
 
void SetMaxDegree (PowerType newMax) throw (std::runtime_error)
 
void SetMinDegree (PowerType newMin) throw (std::runtime_error)
 
bool IsValid () const
 
VariableIndexType GetNumVariables () const
 
PowerType GetPower (VariableIndexType variable) const
 
const PowerType * GetPowers () const
 
const int * GetPowersAsSigned () const
 
void SetPower (VariableIndexType variable, PowerType power)
 
void SetPowers (const PowerType powers[])
 
void CopyPowers (const nmrPolynomialTermPowerIndex &other)
 
void SetDegree (PowerType degree)
 
void GoBegin ()
 
void GoEnd ()
 
void Increment ()
 
void Decrement ()
 
bool IsBegin () const
 
bool IsEnd () const
 
int Compare (const nmrPolynomialTermPowerIndex &other) const
 
bool operator< (const nmrPolynomialTermPowerIndex &other) const
 
bool operator> (const nmrPolynomialTermPowerIndex &other) const
 
bool operator<= (const nmrPolynomialTermPowerIndex &other) const
 
bool operator>= (const nmrPolynomialTermPowerIndex &other) const
 
bool operator== (const nmrPolynomialTermPowerIndex &other) const
 
MultinomialCoefficientType GetMultinomialCoefficient () const
 
MultinomialCoefficientType GetMultinomialCoefficient (PowerType d) const
 
MultinomialCoefficientType CountPowerCombinations () const
 
MultinomialCoefficientType CountLowerOrderTerms () const
 
void SerializeRaw (std::ostream &output) const
 
void DeserializeRaw (std::istream &input)
 
void SerializeIndexRaw (std::ostream &output) const
 
void DeserializeIndexRaw (std::istream &input)
 

Static Public Member Functions

static MultinomialCoefficientType EvaluateMultinomialCoefficient (VariableIndexType numIndices, PowerType chooseFrom, const PowerType indices[])
 
static MultinomialCoefficientType EvaluateMultinomialCoefficient (VariableIndexType numIndices, const PowerType indices[])
 

Protected Attributes

std::vector< PowerType > Powers
 
PowerType MinDegree
 
PowerType MaxDegree
 
int Degree
 

Detailed Description

Represents the power index of a single term in a multi-variable polynomial.

Represents the power index of a single term in a multi-variable polynomial. For example, if the polynomial has four variables, then the power index of the term 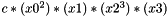$c * (x0^2)*(x1)*(x2^3)*(x3)$ is (2, 1, 3, 1). The power index of the term 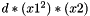$d * (x1^2)*(x2)$ is (0, 2, 1, 0), and so on.

A power index can be used to reference a term in a polynomial, and can also be used as an iterator. We define increment and decrement rules for a power index and they are described in the Compare() method.

To define a complete term in a polynomial, you need at least a pair consisting of a scalar coefficient and a power index. For other forms of polynomials, more parameters are used. For example, for Bernstein basis polynomials, you need a term coefficient, a multinomial coefficient, and the power index.

We define the term power index by the number of variables, the minimal degree, and the maximal degree. This way we can iterate over power indexes within a certain range of degrees. This becomes handy, for example, with Bernstein basis polynomials, where all the terms are of an equal degree. To define a Bernstein term index for n variables of degree d, just create nmrPolynomialTermPowerIndex termIndex(n, d, d);

Note
for runtime efficiency reasons, the current implementation of nmrPolynomialTermPowerIndex caches the degree of the term, that is, the sum of all powers. This means that whenever the index is modified, the sum needs to be updated. Fortunately, this takes a constant number of steps, regardless of the size (number of variables) of the term. Just add the difference between the new variable degree and the old variable degree to the total. Degree comparison is essential to establish the order relation between terms, which later determines where a term is inserted in the polynomial. Therefore we do not want to re-evaluate the degree every time we compare terms for order.

Member Typedef Documentation

typedef unsigned long nmrPolynomialTermPowerIndex::MultinomialCoefficientType

type of a combinatorial result, such as multinomial factor

typedef int nmrPolynomialTermPowerIndex::PowerType

type of a power of a varible – a non-negative integer

typedef int nmrPolynomialTermPowerIndex::VariableIndexType

type of an index to a variable. A variable is x0, x1, x2, ... and the corresponding index is 0, 1, 2, ...

Constructor & Destructor Documentation

nmrPolynomialTermPowerIndex::nmrPolynomialTermPowerIndex ( VariableIndexType  numVariables = 1,
PowerType  minDegree = 0,
PowerType  maxDegree = 4 
)

Ctor: construct a term, defining the number of variables, the minimal degree and the maximal degree. The default values for the parameter are only to enable constructing a default object. Be especially careful with the maxDegree argument, whose default value is arbitrary.

nmrPolynomialTermPowerIndex::nmrPolynomialTermPowerIndex ( const nmrPolynomialBase &  p)

Construct a term valid for a specific Polynomial object

Member Function Documentation

int nmrPolynomialTermPowerIndex::Compare ( const nmrPolynomialTermPowerIndex &  other) const

compare terms according to the order set by the successor function Increment() return zero if the terms are equal, negative value if this term is before the other, and positive value if this term is after the other.

The order relation is quasi-lexicographic. Number of variables is compared first, the greater number of variables has greater term index. Degree is compared next. The greater degree has greater term index. If the degree and number of variables are equal, we compare the individual powers from left to right. The first occurence of unequal powers makes the term index with lower (first different) power greater. That is because the Increment() function "pushes" the power to the right. Then, if term index a has lower power on a left variable than term index b, it means that power was pushed to the left from a to obtain b. That is, b is greater than a.

void nmrPolynomialTermPowerIndex::CopyPowers ( const nmrPolynomialTermPowerIndex &  other)

copy the powers from another term into this one. This operation is valid only if the other term has the same number of variables as this one

MultinomialCoefficientType nmrPolynomialTermPowerIndex::CountLowerOrderTerms ( ) const

Return the number of possible term indices whose corresponding powers are less than or equal to the powers in this term index. The result is the product of all the powers in this term index, adding one to each.

MultinomialCoefficientType nmrPolynomialTermPowerIndex::CountPowerCombinations ( ) const
void nmrPolynomialTermPowerIndex::Decrement ( )

Move to the previous possible term. The rules are the reverse of the Increment() process. That is: 1) Remove all the power from the rightmost positive power, and store it in p. 2) Add 1 to the power of the variable just left of where power was removed. 3) Add (p-1) to the last variable.

For more details, see the Increment() method.

void nmrPolynomialTermPowerIndex::DeserializeIndexRaw ( std::istream &  input)

Deserialize only the power index.

See Also
SerializeIndexRaw().
void nmrPolynomialTermPowerIndex::DeserializeRaw ( std::istream &  input)

Deserialize a power index from a stream. The function should work as the opposite of SerializeRaw().

static MultinomialCoefficientType nmrPolynomialTermPowerIndex::EvaluateMultinomialCoefficient ( VariableIndexType  numIndices,
PowerType  chooseFrom,
const PowerType  indices[] 
)
static
static MultinomialCoefficientType nmrPolynomialTermPowerIndex::EvaluateMultinomialCoefficient ( VariableIndexType  numIndices,
const PowerType  indices[] 
)
static
int nmrPolynomialTermPowerIndex::GetDegree ( ) const
inline

retrieve the degree of the term (sum of all powers). May be negative (!) when the term is invalid

PowerType nmrPolynomialTermPowerIndex::GetMaxDegree ( ) const
inline
PowerType nmrPolynomialTermPowerIndex::GetMinDegree ( ) const
inline
MultinomialCoefficientType nmrPolynomialTermPowerIndex::GetMultinomialCoefficient ( ) const
inline
MultinomialCoefficientType nmrPolynomialTermPowerIndex::GetMultinomialCoefficient ( PowerType  d) const
inline
VariableIndexType nmrPolynomialTermPowerIndex::GetNumVariables ( ) const
inline
PowerType nmrPolynomialTermPowerIndex::GetPower ( VariableIndexType  variable) const
inline

retrieve the power of one variable in the current term. the variable index is zero based!

const PowerType* nmrPolynomialTermPowerIndex::GetPowers ( ) const
inline

return a pointer to the array of all powers.

const int* nmrPolynomialTermPowerIndex::GetPowersAsSigned ( ) const
inline

return the same pointer as GetPowers(), but pointing signed int.

void nmrPolynomialTermPowerIndex::GoBegin ( )

Move to the first possible term of degree MinDegree

void nmrPolynomialTermPowerIndex::GoEnd ( )

Move to the last possible term of degree MaxDegree

void nmrPolynomialTermPowerIndex::Increment ( )

Move to the next possible term. The rule is: 1) Remove all the power from the last variable (index n-1), and store it. 2) Find the rightmost positive power in the remaining term. 3) Move one power from the right of the remaining term to the variable just after. 4) Return the powers from the last variable to the new rightmost positive power.

For example, if we had a term (3, 3, 0, 2) 1) have (3, 3, 0, 0), store 2 2) the last positive degree is of variable #1 (zero based index) 3) change to (3, 2, 1, 0) 4) return the stored 2: (3, 2, 3, 0)

The process is identical if the last power is zero. If in step (2) we are left with no positive powers, we skip the removal of power from the right of the term, and step (3) becomes making the term (1, 0, ..., 0).

bool nmrPolynomialTermPowerIndex::IsBegin ( ) const
inline

tells if this is the first possible term for the given degree limits.

bool nmrPolynomialTermPowerIndex::IsEnd ( ) const
inline

tells if this is the last possible term for the given degree limits.

bool nmrPolynomialTermPowerIndex::IsValid ( void  ) const
inline

return true if the degree of this term is valid, i.e., in the range minDegree..maxDegree

bool nmrPolynomialTermPowerIndex::operator< ( const nmrPolynomialTermPowerIndex &  other) const
inline

decide if this index is before the other according to the successor function Increment().

bool nmrPolynomialTermPowerIndex::operator<= ( const nmrPolynomialTermPowerIndex &  other) const
inline
bool nmrPolynomialTermPowerIndex::operator== ( const nmrPolynomialTermPowerIndex &  other) const

decide if this index is equal to the other. Currently, the operation is not implemented, as it was not needed and its semantics is questionable. Does == mean identity, or does it mean equivalence of index?

bool nmrPolynomialTermPowerIndex::operator> ( const nmrPolynomialTermPowerIndex &  other) const
inline

decide if this index is after the other according to the successor function Increment().

bool nmrPolynomialTermPowerIndex::operator>= ( const nmrPolynomialTermPowerIndex &  other) const
inline
void nmrPolynomialTermPowerIndex::SerializeIndexRaw ( std::ostream &  output) const

Serialize only the power index, without degree limits or number of variables. This function is declared public so that we can save space by calling this one instead of SerializeRaw when serializing a whole polynomial.

void nmrPolynomialTermPowerIndex::SerializeRaw ( std::ostream &  output) const

Serialize the power-index object into a stream. This function is not completely standardized, as the output is in machine-dependent format. Output order is similar to member order.

void nmrPolynomialTermPowerIndex::SetDegree ( PowerType  degree)

Move to the first possible term of the given degree. That is, (degree, 0, 0, ..., 0)

void nmrPolynomialTermPowerIndex::SetMaxDegree ( PowerType  newMax)
throw (std::runtime_error
)
inline
void nmrPolynomialTermPowerIndex::SetMinDegree ( PowerType  newMin)
throw (std::runtime_error
)
inline
void nmrPolynomialTermPowerIndex::SetPower ( VariableIndexType  variable,
PowerType  power 
)
inline

set the power of one variable in the current term. the variable index is zero based!

void nmrPolynomialTermPowerIndex::SetPowers ( const PowerType  powers[])
inline

set all the powers of the term using an array of powers.

Member Data Documentation

int nmrPolynomialTermPowerIndex::Degree
protected
PowerType nmrPolynomialTermPowerIndex::MaxDegree
protected
PowerType nmrPolynomialTermPowerIndex::MinDegree
protected
std::vector<PowerType> nmrPolynomialTermPowerIndex::Powers
protected
The documentation for this class was generated from the following file:
Generated by   doxygen 1.8.6