cisst-saw
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Groups Pages
Classes | Public Types | Public Member Functions | Static Public Attributes | Protected Types | Static Protected Member Functions | Protected Attributes | List of all members
nmrBernsteinPolynomialLineIntegral Class Reference

#include <nmrBernsteinPolynomialLineIntegral.h>

Classes

struct  ProfilingInfo
 
struct  TermSummationElement
 

Public Types

typedef
nmrPolynomialBase::ValueType 		ValueType
 
typedef
nmrPolynomialBase::VariableType 		VariableType
 
typedef
nmrPolynomialBase::VariableIndexType 		VariableIndexType
 
typedef
nmrPolynomialBase::CoefficientType 		CoefficientType
 
typedef
nmrPolynomialBase::PowerType 		PowerType
 
typedef nmrBernsteinPolynomial IntegrandType
 
typedef
nmrPolynomialTermPowerIndex::MultinomialCoefficientType 		MultinomialType
 

Public Member Functions

 nmrBernsteinPolynomialLineIntegral (const IntegrandType &integrand)
 
void UpdateIntegrationTableau ()
 
ValueType EvaluateForSegment (const VariableType p0[], const VariableType p1[], const VariableType gradientNorm, const double roundoffTolerance=DefaultRoundoffTolerance, CoefficientType const *coefficients=NULL)
 
const IntegrandType & GetIntegrand () const
 

Static Public Attributes

static const double DefaultRoundoffTolerance
 

Protected Types

typedef std::vector< PowerType > PowerIndexType
 
typedef std::vector
< TermSummationElement > 		SingleTermIntegrationTableau
 
typedef std::vector
< SingleTermIntegrationTableau > 		PolynomialIntegrationTableau
 
typedef std::vector
< VariableIndexType > 		IndexContainerForZeroVariables
 

Static Protected Member Functions

static ValueType IntegrateSingleTerm (const CoefficientType termCoefficient, const CoefficientType gradientNorm, const nmrPolynomialTermPowerIndex &termIndex, const nmrMultiVariablePowerBasis &powersAtP0, const nmrMultiVariablePowerBasis &powersAtP1, const double roundoffTolerance=DefaultRoundoffTolerance)
 
static ValueType IntegrateSingleTerm (const CoefficientType termCoefficient, const CoefficientType gradientNorm, const PowerType termDegree, const SingleTermIntegrationTableau &termIntegrationTableau, const nmrMultiVariablePowerBasis &powersAtP0, const nmrMultiVariablePowerBasis &powersAtP1, const IndexContainerForZeroVariables &zerosOfP0, const IndexContainerForZeroVariables &zerosOfP1)
 
static void InitializePolynomialIntegrationTableau (const IntegrandType &integrand, PolynomialIntegrationTableau &tableau)
 
static void InitializeSingleTermIntegrationTableau (const nmrPolynomialTermPowerIndex &termIndex, SingleTermIntegrationTableau &termTableau)
 

Protected Attributes

const IntegrandType & Integrand
 
nmrMultiVariablePowerBasis::StandardPowerBasis PowersAtP0
 
nmrMultiVariablePowerBasis::StandardPowerBasis PowersAtP1
 
PolynomialIntegrationTableau IntegrationTableau
 

Detailed Description

class nmrBernsteinPolynomialLineIntegral

Evaluates the line integral of a Bernstein polynomial in n variables. The class is initialized with the integrand polynomial. To evaluate the integral for a segment, call the function EvaluateForSegment() and give the coordinates of two points in n-space between which is the line segment to be integrated.

The integration method iterates for each term of the integrand, and evaluates the integral for the term, then sums all the term integrals together. The following paragraphs should be compiled by LaTex to be visualized as formulas.

For the purpose of this discussion we shall use coordinate indexes starting with 0 instead of the mathematical convention of 1, to correspond to the indexing in C.

Let 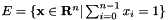$ E = \{\mathbf{x} \in \mathbf{R}^n | \sum_{i=0}^{n-1} x_i = 1\} $ be the ``barycentric'' plane. Let 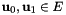$ \mathbf{u}_0, \mathbf{u}_1 \in E $ be two points in the plane. We want to integrate a (Bernstein) polynomial 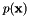$ p(\mathbf{x}) $ along the line segment 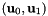$ (\mathbf{u}_0, \mathbf{u}_1) $. For simplicity, we will show here the formula for the integration of a single term of the polynomial, given by 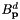$ B_{\mathbf{p}}^{d} $. We know that we can parametrize 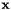$ \mathbf{x} $ in the segment as:

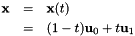
\begin{eqnarray*} \mathbf{x} & = & \mathbf{x}(t) \\ & = & (1-t)\mathbf{u}_0 + t\mathbf{u}_1 \end{eqnarray*}

We note that 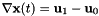$\nabla \mathbf{x}(t) = \mathbf{u}_1 - \mathbf{u}_0$. To evaluate the integral using the parametrized version, we need to multiply the function 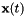$\mathbf{x}(t)$ by the norm of the gradient:

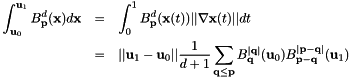
\begin{eqnarray*} \int_{\mathbf{u}_0}^{\mathbf{u}_1} B_{\mathbf{p}}^{d}(\mathbf{x}) d\mathbf{x} & = & \int_{0}^{1} B_{\mathbf{p}}^{d} (\mathbf{x}(t)) || \nabla \mathbf{x}(t) || dt \\ & = & ||\mathbf{u}_1 - \mathbf{u}_0 || \frac{1}{d+1} \sum_{\mathbf{q} \leq \mathbf{p}} B_{\mathbf{q}}^{|\mathbf{q}|} (\mathbf{u}_0) B_{\mathbf{p} - \mathbf{q}}^{|\mathbf{p} - \mathbf{q}|} (\mathbf{u}_1) \end{eqnarray*}

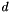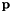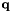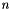where $d$ is the degree of the Bernstein term; $\mathbf{p}$, $\mathbf{q}$ are $n$-length lists of powers of the corresponding variables of the polynomial, s.t. 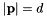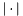$|\mathbf{p}| = d$; $|\cdot|$ is the operator of summing the elements (powers) in the list; and 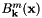$B_{\mathbf{k}}^m(\mathbf{x})$ is the Bernstein term

\[ B_\mathbf{k}^m(\mathbf{x}) = \left( \begin{array}{@{}c@{}} m \\ \mathbf{k} \end{array} \right) x_0^{k_0} x_1^{k_1} \cdots x_{n-1}^{k_{n-1}} \]

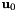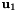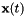The formulas above evaluate the line integral when $\mathbf{u}_0$, $\mathbf{u}_1$, and $\mathbf{x}(t)$ are all in barycentric coordinates. This formula produces erroneous result if we want to compute the integral in the Cartesian space, as it does not take the Cartesian distances into account. For example, consider a tetrahedron with a constant density function. The integral between two points which are given in barycentric coordinates will be the same regardless of the size of the tetrahedron. But for a tetrahedron twice as large, the segment is twice as long, and we integrate the same constant density function over a doubled distance, which should have yielded a doubled integral value. To correct this error, all we need is to re-formulate the gradient. Instead of taking the gradient in barycentric coordinates, we will take it in Cartesian coordinates. 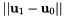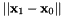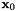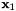Thus the scaling of the integral should change from $||\mathbf{u}_1 - \mathbf{u}_0 ||$ to $||\mathbf{x}_1 - \mathbf{x}_0 ||$, where $\mathbf{x}_0$ and $\mathbf{x}_1$ are the ends of the segment given in Cartesian coordinates.

For an actual development of this formula, see Russ Taylor's technical paper on Bernstein Polynomial Properties.

Note
In the current implementation, we convert directly (using pointer cast) between the types 'nmrMultiIndexCounter::IndexType *' and 'nmrPolynomialTermPowerIndex::PowerType *'. Make sure that the two types are compatible in size.

Member Typedef Documentation

typedef nmrPolynomialBase::CoefficientType nmrBernsteinPolynomialLineIntegral::CoefficientType
typedef std::vector<VariableIndexType> nmrBernsteinPolynomialLineIntegral::IndexContainerForZeroVariables
protected
typedef nmrBernsteinPolynomial nmrBernsteinPolynomialLineIntegral::IntegrandType
typedef nmrPolynomialTermPowerIndex::MultinomialCoefficientType nmrBernsteinPolynomialLineIntegral::MultinomialType
typedef std::vector<SingleTermIntegrationTableau> nmrBernsteinPolynomialLineIntegral::PolynomialIntegrationTableau
protected
typedef std::vector<PowerType> nmrBernsteinPolynomialLineIntegral::PowerIndexType
protected
typedef nmrPolynomialBase::PowerType nmrBernsteinPolynomialLineIntegral::PowerType
typedef std::vector<TermSummationElement> nmrBernsteinPolynomialLineIntegral::SingleTermIntegrationTableau
protected
typedef nmrPolynomialBase::ValueType nmrBernsteinPolynomialLineIntegral::ValueType
typedef nmrPolynomialBase::VariableIndexType nmrBernsteinPolynomialLineIntegral::VariableIndexType
typedef nmrPolynomialBase::VariableType nmrBernsteinPolynomialLineIntegral::VariableType

Constructor & Destructor Documentation

nmrBernsteinPolynomialLineIntegral::nmrBernsteinPolynomialLineIntegral ( const IntegrandType &  integrand)
inline

Member Function Documentation

ValueType nmrBernsteinPolynomialLineIntegral::EvaluateForSegment ( const VariableType  p0[],
const VariableType  p1[],
const VariableType  gradientNorm,
const double  roundoffTolerance = DefaultRoundoffTolerance,
CoefficientType const *  coefficients = NULL 
)

Evaluate the line integral for the segment [p0..p1]. The formulas for the integral are in this class's main documentation.

Parameters
p0first vertex of the segment, given in barycentric coordinates
p1second vertex of the segmend, given in barycentric coordinates
gradientNormthe norm of the gradient, as described in the integration formula. As the inputs to this function are given in barycentric coordinates, the gradient norm must be provided from outside. The user may use the length of the segment in Cartesian coordinates or in barycentric coordinates.
roundoffTolerancea small positive real number. If the absolute value of a variable is <= roundoffTolerance, it is rounded to zero, and reduces the number of iterations required for the integration.
coefficientsif this argument is non-null, then our algorithm uses externally defined coefficients, which are stored in this array. Note that the external coefficients must be in the same order as the ones in the polynomial. See nmrPolynomialBase::EvaluateForCoefficients(). Using external coefficients can improve the runtime efficiency when the integrals are computed with many sets of coefficients, and then the coefficient sets can be cached elsewhere (the polynomial only has one set of coefficients).
const IntegrandType& nmrBernsteinPolynomialLineIntegral::GetIntegrand ( ) const
inline
static void nmrBernsteinPolynomialLineIntegral::InitializePolynomialIntegrationTableau ( const IntegrandType &  integrand,
PolynomialIntegrationTableau &  tableau 
)
staticprotected
static void nmrBernsteinPolynomialLineIntegral::InitializeSingleTermIntegrationTableau ( const nmrPolynomialTermPowerIndex &  termIndex,
SingleTermIntegrationTableau &  termTableau 
)
staticprotected
static ValueType nmrBernsteinPolynomialLineIntegral::IntegrateSingleTerm ( const CoefficientType  termCoefficient,
const CoefficientType  gradientNorm,
const nmrPolynomialTermPowerIndex &  termIndex,
const nmrMultiVariablePowerBasis &  powersAtP0,
const nmrMultiVariablePowerBasis &  powersAtP1,
const double  roundoffTolerance = DefaultRoundoffTolerance 
)
staticprotected

Integration of a single term of the integrand polynomial, using the formula developed above.

Parameters
termCoefficientthe coefficient of the integrand term
gradientNormthe norm of the gradient, which is a constant equal to the distance between the vertices of the segment.
termIndexthe power index of the integrand term
powersAtP0pre-computed power basis for all the variables at the "P0" vertex. In old versions, we used nmrStandardPolynomial as a container for the powers. It is now replaced with the independent object nmrMultiVariablePowerBasis.
powersAtP1pre-computed power basis for all the variables at the "P1" vertex.
roundoffTolerancea small positive real number. If the absolute value of a variable is <= roundoffTolerance, it is rounded to zero, and reduces the number of iterations required for the integration.
static ValueType nmrBernsteinPolynomialLineIntegral::IntegrateSingleTerm ( const CoefficientType  termCoefficient,
const CoefficientType  gradientNorm,
const PowerType  termDegree,
const SingleTermIntegrationTableau &  termIntegrationTableau,
const nmrMultiVariablePowerBasis &  powersAtP0,
const nmrMultiVariablePowerBasis &  powersAtP1,
const IndexContainerForZeroVariables &  zerosOfP0,
const IndexContainerForZeroVariables &  zerosOfP1 
)
staticprotected

Integration of a single term of the integrand polynomial using a pre-computed tableau which stores the power-indices of all the summation elements constituting the term.

Parameters
termCoefficientthe coefficient of the integrand term
gradientNormthe norm of the gradient, which is a constant equal to the distance between the endpoints of the segment.
termDegreethe degree of the integrand term. The product (gradientNorm * (termDegree+1)) is a denominator of the integral.
powersAtP0pre-computed power basis for all the variables at the "P0" vertex.
powersAtP1pre-computed power basis for all the variables at the "P1" vertex.
zerosOfP0indices of the P0 variables which are equal to zero. Summation element in which the power of a zero variable is positive are skipped.
zerosOfP1indices of the P1 variables which are equal to zero.
profileInfo(optional) pointer to a struct that stores inegration profiling.
void nmrBernsteinPolynomialLineIntegral::UpdateIntegrationTableau ( )
inline

As the integrand may change since the initialization of this object, this method lets the user update the integration tableau after changing the integrand (e.g., by adding or removing terms).

Member Data Documentation

const double nmrBernsteinPolynomialLineIntegral::DefaultRoundoffTolerance
static
const IntegrandType& nmrBernsteinPolynomialLineIntegral::Integrand
protected
PolynomialIntegrationTableau nmrBernsteinPolynomialLineIntegral::IntegrationTableau
protected
nmrMultiVariablePowerBasis::StandardPowerBasis nmrBernsteinPolynomialLineIntegral::PowersAtP0
protected
nmrMultiVariablePowerBasis::StandardPowerBasis nmrBernsteinPolynomialLineIntegral::PowersAtP1
protected
The documentation for this class was generated from the following file:
Generated by   doxygen 1.8.6