|
cisst-saw
|
All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Groups Pages
|
cisst-saw
|
#include <cisstNumerical/nmrNetlib.h>#include <cisstVector/vctDynamicMatrix.h>#include <cisstNumerical/nmrExport.h>Go to the source code of this file.
Classes | |
| class | nmrLSMinNorm |
| class | nmrLSMinNorm::Data |
Functions | |
| vctDynamicMatrix< double > CISST_EXPORT | nmrLSMinNorm (vctDynamicMatrix< double > &A, vctDynamicMatrix< double > &b, CISSTNETLIB_DOUBLE r=-1.0) |
| Computes the minimum norm solution to a real linear least squares problem. More... | |
| vctDynamicMatrix< double > CISST_EXPORT | nmrLSMinNorm (vctDynamicMatrix< double > &A, vctDynamicMatrix< double > &b, nmrLSMinNorm::Data &data, CISSTNETLIB_DOUBLE r=-1.0) |
| Computes the minimum norm solution to a real linear least squares problem. More... | |
| vctDynamicMatrix<double> CISST_EXPORT nmrLSMinNorm | ( | vctDynamicMatrix< double > & | A, |
| vctDynamicMatrix< double > & | b, | ||
| CISSTNETLIB_DOUBLE | r = -1.0 |
||
| ) |
Computes the minimum norm solution to a real linear least squares problem.
Computes the minimum norm solution to a real linear least squares problem: 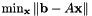
| [in] | A | The 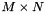 column major matrix. column major matrix. |
| [out] | A | The first 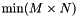 right singular vectors. right singular vectors. |
| [in] | b | The 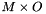 column major matrix. The matrix can be overwritten. column major matrix. The matrix can be overwritten. |
| r | Used to determine the effective rank of A. Singular values 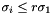 are treated as zero (low rank approximation). If are treated as zero (low rank approximation). If 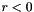 , machine precision is used instead. , machine precision is used instead. |
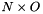 minimum norm solutions
minimum norm solutions 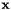 .
. | vctDynamicMatrix<double> CISST_EXPORT nmrLSMinNorm | ( | vctDynamicMatrix< double > & | A, |
| vctDynamicMatrix< double > & | b, | ||
| nmrLSMinNorm::Data & | data, | ||
| CISSTNETLIB_DOUBLE | r = -1.0 |
||
| ) |
Computes the minimum norm solution to a real linear least squares problem.
Computes the minimum norm solution to a real linear least squares problem: 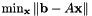
| [in] | A | A 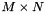 column major matrix. column major matrix. |
| [out] | A | The first 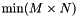 right singular vectors. right singular vectors. |
| [in] | b | A 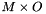 column major matrix. The matrix can be overwritten. column major matrix. The matrix can be overwritten. |
| [in] | data | Provide pre-allocated workspace. If the workspace is not adequate it will be reallocated. |
| r | Used to determine the effective rank of A. Singular values 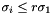 are treated as zero (low rank approximation). If are treated as zero (low rank approximation). If 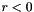 , machine precision is used instead. , machine precision is used instead. |
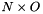 minimum norm solutions
minimum norm solutions 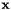 .
.  1.8.6
1.8.6